வாகை மாற்றங்கள் (phase changes) - 5

இருபுனைக் கட்டகங்களின் வாகைப் படத்தை (phase diagram) விவரிப்பதாய்ச் சொல்லியிருந்தேன். இப்போதையத் தொடக்க நிலையில் முழு விவரிப்பும் தந்தால், ஒருவேளை படத்தின் பலக்குமை (complexity)நம்மிற் சிலரைப் பயமுறுத்தக் கூடும். எனவே கொஞ்சங் கொஞ்சமாய் இதை அவிழ்க்கும் வகையில், நீர்ம - ஆவி வாகைகள் மட்டுமிருக்கும் பகுதியை முதலில் விவரிக்கிறேன். கூடவே விழும வளி (ideal gas), விழுமக் கரைசல் (ideal solution) ஆகியவற்றையும் ஓரளவு பார்ப்போம்.

எளிதில் ஆவியாகும் ஈதைல் வெறியம் (A) போன்றதொரு நீர்மத்தை ஒரு கிளராடிக் குடுவையில் (glass flask)எடுத்துக் கொள்வோம். இந்தக் குடுவைக்குள் நீர்மம் இறங்க ஓர் உள்ளீட்டு வாவியும் (inlet valve), ஆவி வெளியேற ஒரு வெளியேற்று வாவியும் (outlet valve), நீர்மம் கீழிறங்க ஓர் இழி வாவியும் (drain valve), குடுவையின் அழுத்தம் (pressure) வெம்மை (temperature) போன்றவற்றை அளக்க வாய்ப்பளிக்கும் இரு துளைகளும் இருக்கட்டும். இத்துளைகளின் வழியே அழுத்தக் கோலும் (pressure gauge), வெம்மை மானியும் (thermometer) செருகியதாய்க் கொள்ளலாம். வேண்டும் வகையிற் குடுவையைச் சூடேற்ற ஒரு சூடேற்றுக் கட்டகம் (heating system) பொருத்தியிருப்பதாய்க் கொள்ளுங்கள்.

குடுவை, கிளராடியிற் செய்ததால், ”உள்ளிருக்கும் கொள்ளீடு (contents) எம் மட்டு (level)?” என்று நம்மால் அளக்க முடியும். இந்தக் காலக் கிளராடிக் குடுவைகள் ஊதுமக் கோளத்திற்கும் (atmosphere) மேல் 2, 3 மடங்கு அழுத்தம் தாங்கும் வலுக் கொண்டவையாதலால், செய்யும் சோதனைகளைத் தாங்கும் ஏமத் திறன் (safety capability) இவற்றிற்கு உண்டு.

ஊதும அழுத்தத்தில் A யின் கொதிநிலை (boiling point) 78.4 பாகை செல்சியசு என்பதால், இவ்வெம்மைக்கருகில் A யைச் சூடேற்றினால் A ஆவி குடுவையிலிருந்து வெளியேறத் தொடங்கும். கூடவே, குடுவையில் இருந்த காற்றும் வெளியேறும். பெருங்கவனத்தோடு செய்தால் ஆவி கலந்த காற்றை குடுவையிலிருந்து வெளியேற்றி A ஆவி மட்டும் அதன் பின் வெளியேறும்படி செய்ய முடியும். அப்போது குடுவைக் கொள்ளீட்டின் வெம்மை 78.4 ஐத் தொட்டு அதற்கு மேற் போகாது ஆவி மட்டும் வெளியேறும்.

இப்பொழுது, வெளியேற்றும் வாவியை மூடினால் குடுவையுள் அழுத்தம் வெளியைக் காட்டிலும் அதிகரிக்கும். குடுவை வெம்மையும் 78.4 பாகைக்கு மேற் செல்லும். குடுவையின் வெம்மை 85 பாகைக்குப் போகிறதென்று வையுங்கள். சூடேற்றும் கட்டக வழி வெம்மையைக் கட்டுறுத்தி (சூட்டைக் கூட்டியோ, குறைத்தோ) குடுவையின் வெம்மை 85 க்கு மேற் போகாதவாறு தொடர்ந்து செய்யலாம். இந்நிலையில் குடுவையின் உள்ளே A யின் இருப்பை அளக்கலாம். இது எடையால் அளந்து மூலகமாய் மாற்றுவதாகவோ, அன்றி குடுவையுள் தெரியும் மட்டத்தின் வழி வெள்ளத்தைக் கணக்கிட்டு மூலகமாய் மாற்றுவதாகவோ அமையும்.

குடுவையின் கொள்ளீடு எவ்வளவு என்று அறிந்த பின், நீர் (W) போன்ற இரண்டாம் பொதியை (ஊதும அழுத்தத்தில் இதன் கொதிநிலை 100 பாகைச் செல்சியசு) உள்ளீட்டு வாவி மூலம் குடுவைக்குள் இறக்கலாம். இரண்டாம் நீர்மத்தின் கொள்ளீட்டு அளவையும் A யை அளந்தது போல் ”எவ்வளவு?” என்றறிந்தால் நம்முடைய அலசலைத் தொடங்கலாம்.

இப்பொழுது குடுவையின் உள்ளே காற்றுக் கிடையாது. குடுவை 85 பாகையில் இருக்கிறது. A பொதியின் மூலக அளவு mA என்றும் W பொதியின் மூலக அளவு mW என்றும் இருப்பதானால் மொத்த மூலக அளவு [mA + mW] என்றாகும். கொடுத்துள்ள கரைசலில் (solution), ஊட்டு மூலகப் பகுவம் (feed mole fraction)

zA = mA/ (mA + mW) என்றாகும்.
zW = mW/ (mA + mW) = 1- zA என்றமையும்.

A, W என்ற பொருள்கள் இரு வாகைகளுக்குள் எங்கும் எப்படியும் விரவி இருக்கலாம். பொதுவாகச் சூடேற்றும் வேகத்தைப் பொறுத்து நீர்ம அளவும், ஆவியளவும் இருக்கும். சூடேறச் சூடேற நீர்மம் குறைந்து எல்லாம் ஆவியாக மாறியிருக்கும். எந்தக் கணத்திலும் நீர்ம மட்டத்தைக் கொண்டு குடுவைக்குள் நீர்மம் எவ்வளவு என்று தீர்மானிக்கலாம். ஒரு குறிப்பிட்ட கணத்தில் நீர்மக் கரைசல் L மூலகம் இருப்பதாகவும், ஆவிக் கரைசல் G மூலகம் இருப்பதாகவும் கொள்ளுவோம். எல்லாக் கணங்களிலும், mA+mW = L+G என்ற சமன்பாடு இருந்து கொண்டேயிருக்கும்.

தவிர, ஆவியில் இருக்கும் A மூலகப் பகுவமும், நீர்மத்தில் இருக்கும் A மூலகப் பகுவமும் ஒன்றுபோல இருக்காது. வெவ்வேறாக இருக்கும். [அவை குடுவைக்குள் உள்ளிட்ட கரைசலின் மூலகப் பகுவத்திலும் இருக்காது.] ஊதும அழுத்தத்தில் A யின் கொதிநிலை 100 பாகை என்றும், W யின் கொதிநிலை 78.4 பாகை என்றுஞ் சொல்லியிருந்தேன். இப்பொழுது 78.4 பாகையைத் தாண்டியவுடன் எது முதலில் ஆவியாகும்? A என்று எளிதில் விடை சொல்ல முடியும். 85 பாகையில் ஆவி வாகையுள் A அதிகமாகவும் W குறைந்தும் இருக்கும். இப்பொழுது A யின் துலைப்பை (balance; துலை என்ற சொல் கருவியையும் துலைப்பு என்ற சொல் கருவி செய்யும் வேலையையும் குறிக்கும்) மட்டும் பார்ப்போம்.

குடுவையுள் இட்ட A யின் மூலக அளவு = mA = (mA+mW)*zA = (L+G)*zA
ஆவி வாகையுள் இருக்கும் A யின் மூலக அளவு = G*yA
நீர்ம வாகையுள் இருக்கும் A யின் மூலக அளவு = L*xA
A யின் துலைப்பைப் பார்த்தால்,
L*xA + G*yA = (L+G)*zA என்றாகும்.
zA = [L/(L+G)]*xA + [G/(L+G)]*yA

இந்தத் துலைப்பை, வாகை வினையின் இயக்கக் கோடு (operating line of the phase reaction) என்று அழைப்போம். கீழே உள்ள முதற்படத்தைக் கவனியுங்கள்.



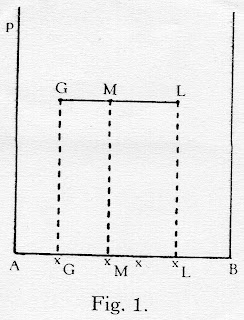
இந்தப் படத்திற் கொடுத்திருக்கும் ஊட்டு மூலகத்தில் (feed moles) குறிப்பிட்ட மூலகப் பகுவம் நீர்ம வாகையில் இருக்கிறதென்றால் அதற்குப் பொருந்தும் மூலகப் பகுவம் ஆவி வாகையில் ஏற்பட்டே தீரும். அதை நம் உகப்பிற்குத் தக்கத் தேரவே முடியாது. அது கட்டகத்தில் ஏற்படும் விளைவு. இப்படி அமையும் இரு வாகைச் செறிவுகளையும் ஒக்கலிப்பு வாகைச் செறிவுகள் (equilibrium phase concentrations)என்று சொல்லுவார்கள். இவை ஒன்றிற்கொன்று ஒக்கலித்தவை. ஒரு வாகைச்செறிவு கூடினால், இன்னொன்றும் அதற்குத் தக்க மாறும்.

நீர்ம, ஆவி வாகைகளில் ஒவ்வொரு சிட்டிகை (sample) பொறுக்கியெடுத்து வேதியலாய்வு மூலமோ, பூதியலாய்வின் மூலமோ இந்த ஒக்கலிப்புச் செறிவுகளை ஆயமுடியும். ஒவ்வோர் ஊட்டுச் செறிவிற்கும் தக்கக் குறிப்பிட்ட நீர்ம, ஆவிச் செறிவுகள் அமையும். குடுவையுள் வெவ்வேறு mA, mW மூலகங்கள் எடுத்து zA என்னும் ஊட்டுச் செறிவை சுழியிலிருந்து ஒன்றுவரை வேறுபடுத்திப் பல்வேறு ஒக்கலிப்பு வாகைச் செறிவுப் புள்ளிகளைத் (xA யும் அதனோடு பொருந்தும் yA யும்) தொடர்ச்சியாகப் பெற முடியும்.

அவற்றைக் கொண்டு, கீழேயுள்ள இரண்டாம் படத்தில் உள்ளது போல் ஒரு திணிவுச் சுருவை (condensation curve) யாகவும், ஓர் ஆவிப்புச் சுருவை (vaporization curve)யாகவும் வரைந்து காட்ட முடியும். திணிவுச் சுருவையை துளி நிலைச் சுருவை (dew point curve) என்றும், ஆவிப்புச் சுருவையைக் கொதிநிலைச் சுருவை (boiling point curve) என்றும் சொல்வதுண்டு.



இங்கே குறிப்பிட்டுள்ள படத்தில், நீர்ம வாகை ஒரு விழுமக் கரைசலாகவும் (ideal solution), ஆவி வாகை ஒரு விழும வளியாகவும் (ideal gas) இருப்பது போற் காட்டப் பட்டிருக்கின்றன. இயலான சுருவைகள் (natural curves) விதம் விதமாய் பலக்குமை (complexity) காட்டி வேறு தோற்றம் கொள்ளலாம். அந்தப் பலக்குமைச் சுருவைகளை அடுத்தடுத்த பகுதிகளிற் காணலாம்.

பொதுவாக ஆவியென்றாலே அது கிடுகுப் புள்ளிக்குக் (critical point) கீழிருப்பது தான் என்றாலும், பலநேரம் நுணுகு வேறுபாட்டை மறந்து வளி(gas)யென்றே சொல்வது உண்டு. பொதுவாக நிலைத்த (constant) வெம்மையில் எந்த வளியின் அழுத்தமும் அதன் திணிவுக்கு (density) நேர் வகுதத்தில் இருப்பதில்லை. பெரும்பாலான வளிகள் இயல்பு மிகுந்த வெம்மையில் (very high temperature), அல்லது மீக்குறைந்த அழுத்தத்தில் (extreme low pressure) கீழுள்ளது போல் நேர்வகுத உறவைக் காட்டுவதுண்டு.

P = R*T*(rho)

இங்கே P என்பது அழுத்தம், R = வளிம நிலையெண் - gas constant, T = கெல்வின் அளவுகோலில் அளக்கப்படும் வெம்மை, rho = வளிமத் திணிவு. எந்தவொரு இயல் வளியும் (natural gas) இந்தப் போக்கை நாம் காணும் அழுத்த, வெம்மை அரங்குகளில் (ranges) முழுதும் காட்டுவதில்லை. அதிக வெம்மை, குறைந்த அழுத்தம் ஆகிய விளிம்புகளில் (boundaries) மட்டுமே இப்போக்கு இயல்பாய்க் காணப்படுகிறது. எனவே விழுமிய (=உயர்ந்த, சிறந்த, பின்பற்றத் தக்க) போக்கான இதை ஒரு போல்மம் (model) போலாக்கி விழும வளி என்று பூதியலார் சொல்லுவார்கள். இயல் வளிகள் அத்தனையும் இவ்விழுமிய போல்மத்திலிருந்து சற்று விலகி விழுமாப் போக்கைக் (non-ideal behaviour) காண்பிக்கின்றன

பொதுவாக, ஒற்றைப் புனைக் கட்டகங்களில் (single component sytems) குறிப்பிட்ட வெம்மையில் மொத்த அழுத்தம் என்பது நீர்மத்தின் ஆவியழுத்தமாகவே இருக்கும். காட்டாகத் தனித்த வெறியமாய் அமையும் போது, P = PA என்றமையும். இதே போல W என்ற நீர்மமும் தனித்து இருக்கும் போது, P = PW என்று காட்டும். இனி வெறியமும் நீரும் கலவையாகும் போது,

A யின் பகுதி அழுத்தம் (partial pressure of A) = xA*PA என்றும்,
W யின் பகுதி அழுத்தம் (partial pressure of W) = (1-xA)*PW என்றும்

அமையும். மேலே காட்டிய பகுதி அழுத்தங்களின் நேர்வகுத வரையறை ரௌல்ட் விதி (Rault's law)யாற் தீர்மானிக்கப் படுகிறது. கூடவே மொத்த அழுத்தம் P = xA*PA + (1-xA)*PW என்று அமைகிறது. இப்படி நேர்வகுதத்தில் அமையும் கரைசலைத்தான் விழுமக் கரைசல் என்று அழைப்பார்கள். இந்தக் கோடும் விழும ஆவிப்புக் கோடு (ideal vaporization line)என்று அழைக்கப் படும். இது மூன்றாவது படத்திற் தெளிவாகக் காட்டப் பட்டுள்ளது.



உண்மையில் வெறியமும் நீரும் கலந்த கலவை ஒரு விழுமக் கரைசல் அல்ல. விழுமக் கரைசலுக்குக் காட்டு வேண்டுமானால் பென்சீன் - தாலுவீன் (Benzene - Toluene) கரைசலைச் சொல்லலாம். 10 பாகை செல்சியசில் அதன் ஆவிப்புக் கோடு விழுமமாகவே இருப்பதைக் கீழே நாலாவது படத்தில் அறியலாம். [இருவேறு நீர்மங்கள் பூதியற் குணங்களில் (physical attributes) ஒன்று போலவே இருந்து, வேதியியற் தாக்கமும் (chemical impact) ஆகக் குறைவாக இருந்து இன்னொரு வகைப் பொதி இருப்பதை உணராத படி உறழ்ச்சி கொண்டிருந்தால் அதை விழுமக் கரைசல் என்று சொல்லுவார்கள்.]



நீர்ம வாகை விழுமக் கரைசலாய் இருந்து, ஆவி வாகை விழும வளியாக இருக்கும் போது, ஒக்கலிப்புச் சமன்பாடு,

yA = xA*PA/P என்றும்,

ஆவி மூலகப் பகுவத்தின் வழி, மொத்த அழுத்தம், 1/P = yA/PA + (1-yA)/PW என்றும் அமையும். மொத்த அழுத்தச் சமன்பாடு ஒரு செவ்வக மீவளைவுச் சுருவையை (rectangular hyperbolic curve) உணர்த்தும். விழுமத் திணிவுச் சுருவை (ideal condensation curve) இப்படித்தான் தோற்றம் காட்டுகிறது.

மேலேயுள்ள இரண்டாம் படத்தில் P என்பதை குத்துக்கோட்டு (vertical) அளவுகோலாகவும், x/y/z போன்ற மூலகப் பகுவங்களை கிடைக்கோட்டு (horizontal) அளவுகோலாகவும் கொண்டு விழுமத் திணிவுச் சுருவையும் , விழும ஆவிப்புச் சுருவையும் காட்டப் பட்டிருக்கின்றன. இரண்டும் A,W என்ற பொருள்களின் இருவேறு ஆவியழுத்த எல்லைப் புள்ளிகளிற் சந்தித்துக் கொள்கின்றன. மொத்தத்தில் இரு சுருவைகளும் சேர்ந்து ஓர் இலை போலத் தோற்றம் காட்டுவதைக் காணலாம். இரு சுருவைகளையும் குறுக்கே வெட்டுவது போல் ஓர் இயக்கக் கோடும் காட்டப் பட்டிருக்கிறது. இயக்கக் கோட்டைக் குறுக்கு வெட்டும் இன்னொரு குத்துக் கோடும் காட்டப் பட்டிருக்கிறது. இந்தக் குத்துக் கோடு ஒரு குறிப்பிட்ட ஊட்டுச் செறிவோடு ஒரு கலவையை மேலிருந்து கீழே கொண்டுவரும்போது முதலில் முழுக்க நீர்மமாய் இருந்து பின் நீர்ம, ஆவி வாகைகளாய்ப் பிரிந்து வெவ்வேறு ஒக்கலிப்புச் செறிவுகளைக் காட்டி முடிவில் முழுக்க ஆவியான செலுத்தத்தைக் (process) காட்டுகிறது.

இரண்டாம் படத்தைக் கூர்ந்து கவனிக்க வேண்டுகிறேன். .

அன்புடன்,
இராம.கி.